
• De palabras a vectores: la proximidad semántica como interfaz de comprensión
Proximidad semántica
Índice
- Contexto
- Explicación del concepto / teoría
- Aplicaciones actuales y relevancia
- Ejemplo práctico: Kotlin + PGVector
- Limitaciones y debates
- Conclusión / síntesis
- Fuentes y lecturas recomendadas
Antes de que los niños aprendan a definir conceptos con precisión, ya pueden agrupar objetos por “parecidos”. Un niño pequeño, al procesar la información sensorial y simbólica que recibe, tiende a colocar al perro y al gato en una región próxima dentro de su interpretación del mundo. Por eso, los llama igual. No es exactamente un error: podríamos considerarlo una forma temprana de razonamiento por similitud, una intuición primitiva de lo que hoy entendemos como proximidad semántica.
En su estudio longitudinal, considerado seminal en el campo, Similarity, Specificity and Contrast (1986), Dromi y Fishelzon observaron que los niños categorizan el mundo no por definiciones fijas, sino por relaciones de similitud difusa. Lo que hoy la inteligencia artificial hace con vectores, el cerebro lo intuyó desde la infancia: lo similar se agrupa, aunque no se nombre igual.
Esa intuición es ahora tecnología: la proximidad semántica permite que los sistemas modernos “entiendan” más allá del texto literal. Este salto se dio cuando el lenguaje dejó de procesarse como texto plano y empezó a modelarse como vectores numéricos en espacios de alta dimensión. Modelos como word2vec, GloVe o BERT aprendieron a representar significados en coordenadas, permitiendo que operaciones matemáticas aproximen relaciones semánticas. Así, lo que antes era interpretación difusa, hoy se transforma en cálculo sobre distancias. ¿Cómo se modela eso? ¿Cómo lo usamos en software real?
Contexto
El concepto de similitud semántica no es nuevo. En lingüística computacional, ya en los años 50 se hablaba de coocurrencia de términos y análisis de contexto. Pero luego vinieron varios saltos clave:
- word2vec (2013): permitió representar palabras como vectores que capturan similitudes de contexto. Gracias a ello, conceptos relacionados aparecen cerca en un espacio vectorial, permitiendo incluso operaciones como
king - man + woman ≈ queen. https://es.wikipedia.org/wiki/Word2vec - BERT y modelos posteriores: llevaron la idea más allá al generar vectores que dependen del contexto en que aparece cada palabra, permitiendo una comprensión más precisa y matizada del lenguaje. https://es.wikipedia.org/wiki/BERT_(modelo_de_lenguaje)
Esto abrió una nueva vía: si el significado puede representarse como un punto en el espacio, entonces la distancia entre puntos es una medida de similitud
Explicación del concepto / teoría
La proximidad semántica mide qué tan cerca están dos elementos en un espacio vectorial entrenado para capturar significados. Algunos principios clave:
- Embeddings: Representación numérica de palabras, frases o documentos en un espacio de N dimensiones.
- Métricas de distancia
- Espacio semántico: Un espacio donde “gato” está más cerca de “felino” que de “refrigerador”.
Ejemplo:
import kotlin.math.sqrt
fun main() {
val cat = listOf(0.1, 0.3, 0.5)
val dog = listOf(0.12, 0.1, 0.52)
val cosSim = cosine(cat, dog)
println(cosSim)
}
fun cosine(a: List<Double>, b: List<Double>): Double {
val dotProduct = a.zip(b).sumOf { (x, y) -> x * y }
val magnitudeA = sqrt(a.sumOf { it * it })
val magnitudeB = sqrt(b.sumOf { it * it })
return if (magnitudeA != 0.0 && magnitudeB != 0.0) {
dotProduct / (magnitudeA * magnitudeB)
} else {
0.0
}
}El valor de cosSim cercano a 1 indica alta similitud semántica. La métrica del coseno es una de las más utilizadas para calcular esta proximidad porque mide el ángulo entre dos vectores, ignorando su magnitud. Esto resulta útil cuando lo importante es la dirección (es decir, el patrón semántico), no la intensidad.
Existen otras métricas posibles, como la distancia Euclídea (que mide la distancia lineal entre dos puntos en el espacio) o la distancia Manhattan (que suma las diferencias absolutas en cada dimensión).
Sin embargo, en espacios de alta dimensión como los generados por embeddings, el coseno suele ser más estable y representativo: penaliza menos los vectores largos y tiende a funcionar mejor cuando los datos están normalizados. Por eso, es la opción por defecto en la mayoría de sistemas de búsqueda semántica.
Aplicaciones actuales y relevancia
¿Para qué sirve esto en software moderno?
- Recomendadores: mostrar contenido similar a lo que el usuario ya vio.
- Búsqueda semántica: más allá de keywords exactas.
- Clasificación: identificar intenciones o temas aunque no haya coincidencia textual.
- Grafo del conocimiento: encontrar conexiones entre ideas o conceptos.
En desarrollo backend con Kotlin y PostgreSQL, podemos usar pgvector para almacenar y consultar estos vectores eficientemente.
Ejemplo práctico: Kotlin + PGVector
Supongamos que tienes una tabla text y cada entrada tiene un campo embedding de tipo vector(768). Este tamaño no es arbitrario: corresponde al tamaño del embedding generado por el modelo nomic-embed-text, que puedes usar para representar textos con un vector numérico de 768 dimensiones.
Primero creamos la tabla y un índice HNSW para optimizar la búsqueda por similitud:
CREATE EXTENSION IF NOT EXISTS vector;
CREATE TABLE text (
id UUID PRIMARY KEY,
content TEXT,
embedding vector(768)
);
CREATE INDEX idx_embeddings_hnsw_cosine
ON text
USING hnsw (embedding vector_cosine_ops);La consulta en Kotlin usando Spring Data JPA sería:
@Query(
value = """
SELECT content AS text,
1-(embedding <=> CAST(:embedding AS vector)) AS score
FROM text
ORDER BY embedding <=> CAST(:embedding AS vector) DESC
LIMIT :limit
""",
nativeQuery = true,
)
fun findMostSimilar(
@Param("embedding") embedding: String,
@Param("limit") limit: Int = 5,
): List<Text>Aquí usamos el operador <=> de PGVector, que mide distancia por similitud coseno. Es diferente del operador <#>, que mide distancia euclídea. Mientras <#> penaliza la magnitud del vector (distancia lineal), <=> se enfoca en la dirección, lo que lo hace más adecuado para comparar significados.
Puedes ver un ejemplo completo en este repositorio: github.com/apascualco/semantic-search
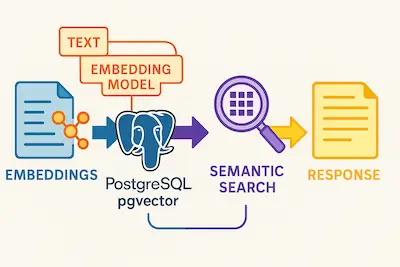
Diagrama de flujo de una búsqueda semántica
Limitaciones
- Black-boxing: los embeddings pueden capturar sesgos del modelo.
- Dimensionalidad: más dimensiones ≠ mejor resultado.
- Actualización: ¿qué pasa si cambian los significados o el contexto?
- Contexto vs. significado universal: un embedding no siempre refleja la intención real de una frase ambigua.
Conclusión / síntesis
La proximidad semántica es hoy la piedra angular de sistemas inteligentes que entienden, recomiendan y conectan. Su fuerza radica en convertir el lenguaje en geometría, y la lógica en distancia. Como desarrolladores, integrar esta capa nos permite construir productos que “comprenden” más allá del texto.
Fuentes y lecturas recomendadas
- Mikolov et al. (2013). Efficient Estimation of Word Representations in Vector Space.
- pgvector: vector similarity search for Postgres
- The Illustrated Word2Vec
- Dromi, E. & Fishelzon, A. (1986). _Similarity, Specificity and Contrast
